ダダサバイバーの課金要素にマンスリーパスがあります。
- マンスリーパス
- 高級マンスリーパス
の2種類が用意されています。
毎日報酬が貰えるパスですが、期限がいつなのか?お得なのか?わかりませんよね。
今回はマンスリーパスについて紹介します。
マンスリーパスの期限/期間は購入日を含めた30日
購入日を含めた30日がマンスリーパスの期限。
30日後に解約されます。

実際にマンスリーパスを購入してみると

残り日数が29日になりました。
購入日を含めた30日間マンスリーパスを利用することができます。
マンスリーパスの日数は深夜1時に更新される
マンスリーパスの日数が更新されるのは、購入した時間ではなく深夜1時に更新されます。
ダダサバイバーが更新される時間の1時に合わせられます。
つまり、マンスリーパスを購入するときは、深夜1時1分に購入するとお得です。
マンスリーパスの報酬内容
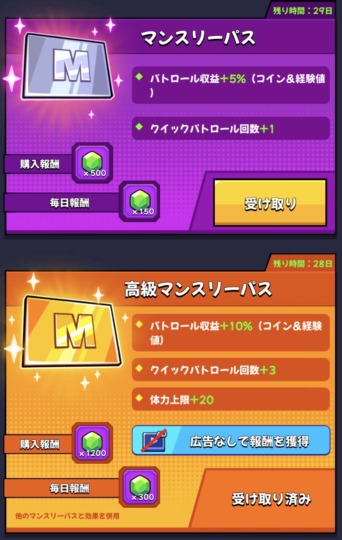
30日間利用できるマンスリーパスですが、報酬内容が高級と通常でちがいます。
料金:
iOS 800円
Android 680円

- 購入報酬500ジェム
- パトロール収益+5%(コイン&経験値)
- クイックパトロール回数+1
- 毎日報酬150ジェム
30日間で
- クイックパトロール+30回
- 購入報酬を含め合計5000ジェム
受け取れます。
料金:
iOS 1,600円
Android 1,380円

- 購入報酬1200ジェム
- 広告なしで報酬を獲得
- パトロール収益+10%(コイン&経験値)
- クイックパトロール回数+3
- 体力上限+20
- 毎日報酬300ジェム
30日間で
- クイックパトロール+90回
- 購入報酬および広告ジェムを含め12000ジェム
受け取れます。
マンスリーパスで5000ジェム、高級で10200ジェム入手することができ、毎日遊ぶ人にとって非常にお得です。
高級マンスリーパスは広告なしで報酬を獲得できる為
- 特別行動の更新2回
- スタミナ回復3回
- デイリーショップの30ジェム2回
- コイン1回
- ゲームオーバー時の復活1回
の広告でできる事を見ずに行えます。
マンスリーパスは課金におすすめ?
結論から言うと、課金するならマンスリーパスがおすすめです。
ジェムを通常課金する場合
| ジェム(初回2倍) | iOS値段 | Android値段 |
|---|---|---|
| 80(160) | 160 | 140 |
| 500(1000) | 800 | 680 |
| 1200(2400) | 1,600 | 1,380 |
| 2500(5000) | 3,200 | 2,760 |
| 6500(13000) | 8,000 | 6,900 |
| 14000(28000) | 15,800 | 13,800 |
マンスリーパスは30日合計500ジェム、高級マンスリーパスで合計10200ジェムです。
普通に課金しようとすると、
- 初回2倍で2500ジェムがマンスリーパス分
- 初回2倍で6500ジェムが高級マンスリーパス分くらい
マンスリーの課金額の倍以上かかってしまいます。
すぐにガチャを回す予定がないなら、マンスリーパスはコスパよくおすすめです。
購入するなら高級マンスリーパスがコスパ○
仮に購入するなら高級マンスリーパスがコスパが良いです。

- 購入報酬1200ジェム
- 広告なしで報酬を獲得
- パトロール収益+10%(コイン&経験値)
- クイックパトロール回数+3
- 体力上限+20
- 毎日報酬300ジェム
- 購入報酬を含め合計10200ジェム
と内容が豪華です。
特に広告を見ずにジェムを60受け取れるのもあるので、実質合計12000ジェム手に入れることができます。
広告がフリーになるのは非常に便利で、快適にゲームが遊べます。
マンスリーパス評価まとめ
購入日を含めた30日がマンスリーパスの期限。
30日後に解約されます。
料金:
iOS 800円
Android 680円
- 購入報酬500ジェム
- パトロール収益+5%(コイン&経験値)
- クイックパトロール回数+1
- 毎日報酬150ジェム
30日間で
- クイックパトロール+30回
- 購入報酬を含め合計5000ジェム
受け取れます。
料金:
iOS 1,600円
Android 1,380円
- 購入報酬1200ジェム
- 広告なしで報酬を獲得
- パトロール収益+10%(コイン&経験値)
- クイックパトロール回数+3
- 体力上限+20
- 毎日報酬300ジェム
30日間で
- クイックパトロール+90回
- 購入報酬および広告ジェムを含め12000ジェム
受け取れます。
購入するなら高級マンスリーパスがコスパ良いですが、マンスリーなので30日間のみとなります。
毎月高級マンスリーパスを課金するとiOSで年間14,400円かかる計算です。